By Ferenc Bodon Ph.D.
KX guest blogger Ferenc Bodon is an expert kdb+ programmer and an experienced software developer in several other programming languages, as well as a software architect with an academic background in data mining and statistics. KX has previously re-published other articles by Ferenc, A comparison of Python and q for data analysis and A comparison of Python and q for handling lists. Follow Ferenc on LinkedIn, where he writes about programming language comparisons and originally published this article with the title Data Analysis by Python and Q.
In this article, I take a simple, real-life problem and analyze different solutions in Python and q. The problem is magical in the sense that unraveling it leads us to discover nice areas of these two programming languages including vector operations, Einstein summation, adverbs and functional form of select statements. Each solution has lessons to learn that deepens our IT knowledge, especially if we consider performance aspects as well. I believe that people understand programming concepts better via examples.
Python and q are two world-class, dynamic programming languages with many similarities and some interesting differences. Python is a general language with specialized libraries for different fields like web and mobile development or data analysis. Q is primarily used in the financial industry for data analysis and developing trading algorithms. On Wall Street, people often use these tools side-by-side, sporadically with R and Matlab.
Problem Statement
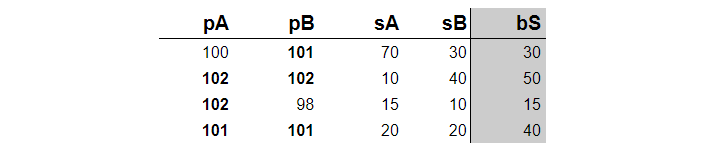
We have a table of bid prices and sizes of two buyers. Bid price p with size s means that the buyer is open to buy s number of product at price p. We have a table of four columns:
- bid prices offered by the two buyers, pA and pB.
- bid sizes, sA, and sB.
Our job is to add a new best size column (bS) to the table, that returns the size at the best price. If the two buyers have the same price then bS is equal to sA + sB, otherwise, we need to take the bid size of the buyer that offers a higher price.
An example table with the desired extra column is below. The best prices are in bold.
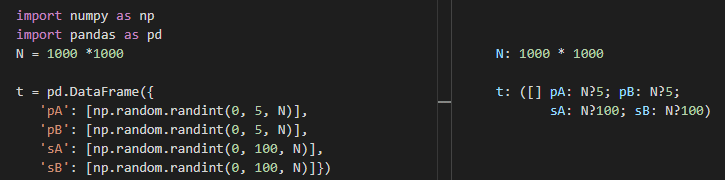
The task sounds simple. To appreciate this article, you should stop here and come up with at least two solutions and also try to generalize the task in several ways. The following code lines generate a random table t to play with.
An elementary solution
Complex problems need to be decomposed into simple problems that are easier to solve. So let us forget about the table and take a single row with prices pA, pB and sizes sA and sB. To get the best sizes, we can come up with a function including two IF-THEN-ELSE statements (denoted by operator $ in q).

Function bestSizeIF can be applied to each row of table t.

A more elegant solution
The more experienced programmer you are, the less IF statements you use and replace conditions with proper design principles. IF-THEN-ELSE statements create a condition in the logic that splits the execution path into two branches. The human brain and the processor architectures prefer sequential execution, operations followed by operations… similarly, as we read a book, line-by-line. Can we get rid of the IF statements completely?
Let us derive a Boolean vector that is true at position i if the iᵗʰ price is maximal. We prepare for the general case when we have more than two buyers. We can easily get the maximal price by function max (aka. amax in Numpy). Maximal value can be compared to all elements of the price vector. We make use of the vector processing nature of Numpy and q. In statement x == y, a vector is returned if either x or y (or both with the same length) is a vector. Q uses = for comparison.
Based on the Boolean vector we can follow two approaches. On the one hand, we can get the indices of True values and use these to index the size vector and finally calculate a sum. Again, both Numpy and q can index a vector with another vector. Furthermore, in both languages the where function returns a list of indices containing True values. Q saves some typing by letting you omit square brackets for indexing.

In the other approach, we rely on Boolean arithmetic in which True acts as one, False acts as zero. We can replace the where statement and the indexing with a simple vector multiplication.

Multiplying two vectors then summing the result is the weighted sum (inner product). We can simplify our code by leveraging built-in weighted sum functions which are np.dot/np.inner in Python and wsum in q.

The final solution was proposed by András Dőtsch. It is elegant and performant. Its efficiency is coming from the fact that a weighted sum for vectors of sizes two can be replaced by simple addition and the two weights can be derived by two comparisons.
![]()
Observe the different usage of parentheses. There is operator precedence in Python. Developers need to remember that comparison has lower precedence than multiplication. In q the expression is evaluated from right to left.
Performance
Let us stop for a bit and compare the performance of the four approaches. The table below contains execution times in seconds on a sample table of size one million. Prices were random numbers between one and five. Tests were executed a hundred times. I used q version 3.6, Python 3.4.4. Tests ran on a 64 bit, Red Hat Linux server with kernel version 3.10.0 and CPU Intel Xeon E5-2650 v4 @ 2.20 GHz.
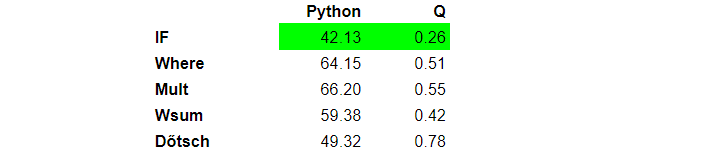
Function with IF statement is the fastest as it does not need to create a temporary variable p, which requires memory allocation. Although we played with vector operations, we don’t gain many benefits of it for vectors of size two.
Q is two orders of magnitude faster than Python.
Vector Programming
We took a step toward vector programming by refactoring function bestSize. The input of the function is still scalars and we get the final result by applying a scalar function to four scalars obtained from four lists. If the input table contains one million rows, then we execute function bestSize one million times. Every single function call has a cost. Can we improve our function to accept four lists instead of four scalars and execute the function just once?
Numpy and q support vector conditionals. Instead of using functions if and $ for IF-THEN-ELSE we can use the three-parameter version of np.where and ? in q. Operator + works well on vectors and performs element-wise addition in both languages.

Unless the helper function is used multiple times or it helps readability, you can drop it completely and use a simple and stateless expression.
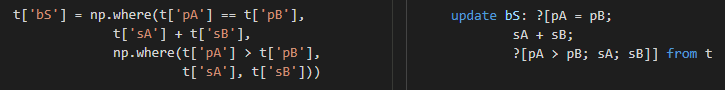
Vector multiplication is supported by both Numpy and q. We can rewrite bestsizeMult in two ways. Either we store prices and sizes in a list of pairs or in a pair of lists, i.e in a matrix of size N x 2 or 2 x N. We need to choose the proper shape based on the internal representation of the matrix and the operation we would like to perform on it. Traversing an array is faster if CPU can process the data sequentially and CPU caching is fully utilized.
Numpy stores matrices in row-major order (aka. C-style), q stores matrices in column-major order (aka. Fortran style). This implies that in our task, Numpy prefers shape N x 2, q prefers shape 2 x N. For comparison, I will provide q syntax and performance metric for the suboptimal solution.
In Python we need to employ the axis parameter of np.amax/np.max and np.multiply instead of * to handle vectors:
In q we need to use a simple adverb. Function each applies a monadic function on each element of a vector (similarly as function map in Python). Operator * can remain intact – it handles lists and scalars, as expected. To create a list of pairs, we can transpose (function flip) a pair of two vectors.

Working with pairs of lists differs slightly.

In this approach, we rely on the polymorphic nature of q functions. For example, the function max returns the maximal element if a list is provided as input. For matrices, it returns the maximal value of each column. The same applies to the function sum. We can use adverb each to use monadic functions on each row instead of on each column. For binary functions, we use adverb each left left and each right – denoted by \: and /: respectively.
The second version of function bestSizeMult_V saves two expensive matrix transpose, hence runs faster.
We can simplify the code again by merging the multiplication and summation into a weighted sum method. In Numpy we need yet another function called einsum that implements Einstein summation. In q we can leverage wsum again as it automatically applies weighted sum to each corresponding column if the parameters are two matrices.

Function bestSizeDotsch is the only one that does not need to be updated to accept four-vectors instead of four scalars. Operations that it uses, i.e. comparison, multiplication, and addition all work seamlessly on scalars and vectors.
Performance
The run times of the vector-based approaches are in the table below.
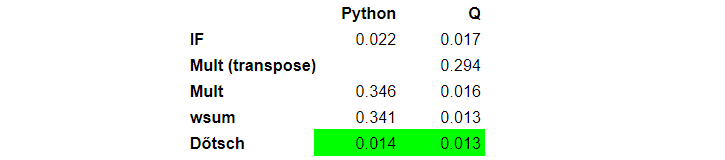
We can see that vector-based approach speeds up Numpy-based solution by two orders of magnitude. The vector conditional feature of Numpy and q are very powerful, they yield super fast solutions.
Generalization
What happens if a new buyer (denoted by C) shows up on the market? We can get prices from three sources. The super fast IF-THEN-ELSE approach becomes ugly since the number of branches increases exponentially – from three to seven in our case. Similarly, we cannot extend function bestSizeDotsch. In the general problem, we are given a table and a list that stores the names of price columns and another list that stores the names of size columns.
First, we investigate how we need to change the two buyers’ case if the columns are not hardcoded but provided in parameters. Let us stick to the weighted sum solution and do a minor refactoring. Instead of accepting two vectors (pA and pB), we need a pair of vectors, i.e. a vector of vectors, aka. matrix.
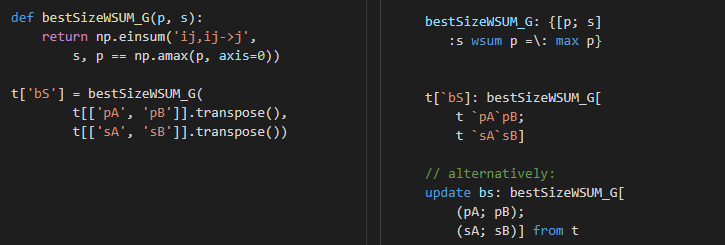
Generalizing the code from here is trivial. When selecting a list of columns we can provide a list of column names.

Q allows developers to follow the same approach that Python does. Furthermore, we can use select/update statements that often provide faster and more readable code than Pandas equivalent. For completeness, I also provide a general version of the select/update-based solution.
In q the column names are part of the update statement. If you need the flexibility of accepting a symbol list like `pA`pB`pC and you need an expression (pA; pB; pC) then you need to employ an advanced technique called the functional form of an update. In reality, every select and update statement translates to a functional select/update statement. For example, the simple update statement
![]()
translates to
![]()
The exclamation mark with four parameters stands for the update statement. The first parameter is the table, then the list of WHERE constraints – empty list if there is no filtering. The third parameter is the group-by option – false if grouping is not required. The last parameter is a dictionary with the keys of the new column names and values with the parse-tree expression to get the new columns. In our example, we update a single column. You can create a list of size one by function enlist.
We can get the functional form of a select/update statement by employing helper function parse or buildSelect.

Without in-depth knowledge of parse trees, we can figure out that we simply need to prepend command enlist to the list of price and size column names to get the functional form of the update statement we are looking for.

Performance
In my final experiment, I checked how the two languages scale if the number of columns increases. Numpy and q scale in a similar way and q is a few times faster than Numpy.

Conclusion
I’ve presented a simple data analytics problem and went through solutions in Python and q at various expertise levels. Junior developers are able to come up with a simple and readable IF-THEN-ELSE based solution, that is two orders of magnitude faster in q than in Python. Intermediate developers who know vector operations come up with an even faster and readable solution. Numpy’s and q’s solutions are very similar both in syntax and performance.
Solving the general problem requires Boolean arithmetic and vector operations. In q, we can use operators like *, max, and wsum. In Numpy, we need to drop * and dot and pick up multiply and einsum as soon as we move from simple vectors to vector of vectors. This resonates with the different design principles of q and Python. In q, there are powerful and orthogonal tools, which you can plug together to solve complex problems. In Python, there are far more functions and parameters, orthogonality is less of a concern. Also, developers need to type
Q also allows developers to use select/update statements. If the column names are coming from parameters then we need to know the functional forms of the select/update statement. With helpers of parse and buildSelect even an intermediate q developer will come up with the proper solution. However, programmers with expertise in other common programming languages are less likely to be able to read, support and modify the q code.
Acknowledgments
I would like to thank Péter Györök and Andrew Wilson – two black belt q masters – for their valuable feedback.












