By Christopher Brandt
This week we are re-blogging a technical paper by Christopher Brandt, an engineer at NAG, which describes how to use the NAG library with kdb+. The NAG Library is the world’s largest collection of robust, documented, tested and maintained numerical algorithms that are sold by the Numerical Algorithms Group. Christopher’s article was originally published on the NAG blog, and is also available here. This version of the report has been edited for style.
Introduction
In this report we demonstrate how to integrate the NAG Library with kdb+ using the Foreign Function Interface (FFI) from KX. The procedure outlined herein leverages FFI to drastically simplify the development process for users. The enclosed three examples were carefully chosen to illustrate usage cases that extend to most of the 1700+ routines contained within the NAG Library.
NAG and KX share a number of customers, many of whom use the NAG Library with the q programming language. Within this report, we describe a procedure for using the NAG Library with kdb+ in a pure q environment that will enable developers to write less code, employ fewer development tools, and shorten overall development time.
NAG and KX
This is not our first technical report describing how to use the NAG Library with kdb+. Please refer to the NAG Blog article titled Calling the NAG C Library from kdb+, written by Brian Spector, for additional information. Readers may also find the NAG Blog article C++ Wrappers for the NAG C Library, also written by Brian Spector, to be a good complement to this report.
Foreign Function Interface from KX
The Foreign Function Interface (FFI) from KX enables the linking of dynamic libraries in a pure q environment by using several functions defined within the FFI namespace. In this report, we will employ these functions to invoke each NAG Library routine individually, and their usage will be detailed within each example below. Note that you must work with the shareable version of the NAG Library when calling NAG routines directly within q.
At the time of writing, FFI is not compatible with NAG Library routines that require user-defined callback functions written using pure q. NAG has been working with KX to extend FFI to provide a simple, yet robust, solution to accommodate callbacks, and the results of that work will be detailed in a subsequent paper. Presently, we recommend that kdb+ users wishing to utilize NAG Library routines that require callback functions follow the procedure outlined in the NAG Blog Calling the NAG Library from kdb+.
NAG Alternative C Interface
The NAG Library provides two interfaces for the C programming language. The first interface, known as the NAG C Library, employs C structs and enums to ensure type correctness and interface consistency across 1700+ routines. The second interface, known as the alternative C interface, uses only C intrinsic types as arguments for each routine. Since q is an array-based query language and lacks the internal framework to create user-defined types that are compatible with comparable C structs and enums, we recommend that kdb+ users work with the alternative C interface to the NAG Library.
Originally serving as the C interface to the NAG Fortran Library, the alternative C interface is available with the NAG C Library beginning with the Mark 26.2 release. The documentation for this interface appears within the NAG Fortran Library documentation.
This interface uses several typedefs to maintain compatibility for multiple NAG C Library implementations across various operating systems and hardware architectures, and we highlight the most commonly used typedefs below:
- Integer: basic integer type, resolves to a 32-bit or 64-bit C integer type (e.g. int or long) depending on the implementation
- Charlen: character length argument for associated character arrays, resolves to the same C intrinsic type as Integer
- NAG_CALL: only necessary when working with user-defined callback routines for certain implementations of 32-bit Windows distributions; contact NAG support for details
NAG C Library Implementations
Multiple implementations of the NAG C Library are released to accommodate various operating systems (Linux, Windows, macOS), hardware architectures (Intel 32-bit, Intel 64-bit), and data models (LP64, ILP64, IL32P64, etc.). Accordingly, a kdb+ user incorporating the NAG C Library into their program will need to select the appropriate q integer size that corresponds to their chosen NAG C Library implementation. The example code contained within this report is compatible with the Mark 26.2 release of the NAG C Library for 64-bit Linux with 64-bit Integers and 64-bit Pointers (product code CLL6I262DL). The q scripts for the following examples are available on the NAG GitHub webpage, along with example scripts for two other widely used NAG C Library Mark 26.2 implementations: (1) 64-bit Windows with 32-bit Integers and 64-bit Pointers (product code CLW6I262EL), and (2) 64-bit Linux with 32-bit Integers and 64-bit Pointers (product code CLL6I262CL).
Examples
The following three examples demonstrate how to call NAG C Library routines using the alternative C interface with q and FFI. These examples were carefully selected, as they will mirror the majority of usage cases a customer will encounter across all 1700+ routines within the library. If your usage case falls outside of these three examples, please contact NAG support for assistance.
Example 1: BLAS Routine DAXPBY
Our first example, which follows closely to the BLAS example from the FFI documentation, requires only integer and floating-point type arguments to perform the operation.
Below is the alternative C interface signature for NAG Library routine f16ec (BLAS routine DAXPBY), which requires three Integers, two doubles, and two arrays of doubles.
void f16ecf_ (
const Integer *n,
const double *alpha,
const double x[],
const Integer *incx,
const double *beta,
double y[],
const Integer *incy
)Within our q script, we begin by first loading the FFI namespace into our q environment using the following statement:
/ Load FFI namespace
\l ffi.qTo satisfy the signature for our function, we define all scalar arguments as vectors with one element (i.e. a pointer to the appropriate type). When these arguments are passed by value to the routine, the address of the vector’s first element is copied to the parameter, thereby satisfying the signature for our routine (e.g. the vector decays into a pointer). For this specific routine, we are working only with objects of type Integer and type double.
/ Parameters
n:1#5j
alpha:1#3.0f
x:5#-6.0 4.5 3.7 2.1 -4.0f
incx:1#1j
beta:1#-1.0f
y:5#-5.1 -5.0 6.4 -2.4 -3.0f
incy:1#1jTo call the NAG routine using pure q, we invoke the cf function from the FFI namespace, followed by the argument list for the NAG routine. The cf function itself receives two arguments: (1) a char containing the return type for the chosen routine (or ” “ for a void function), and (2) the symbol name of the routine we wish to invoke. Note that the symbol name of the routine includes the name of the shared object in which it is located.
Example Two: Nearest Correlation Matrix
/ Call NAG routine f16ec
.ffi.cf[(" ";`libnagc_nag.so`f16ecf_)](n;alpha;x;incx;beta;y;incy)Our collection of nearest correlation matrix routines is one of the more popular sections of the NAG Library. As such, our second example will demonstrate how to call NAG Library routine g02ab to compute the nearest correlation matrix X by minimizing the weighted Frobenius norm:
![]()
where G is an approximate correlation matrix and W is a diagonal matrix of weights.
This example expands upon the first by including a char array as an argument. The alternative C interface signature for this routine is defined below.
void g02abf_ (
double g[],
const Integer *ldg,
const Integer *n,
const char *opt,
const double *alpha,
double w[],
const double *errtol,
const Integer *maxits,
const Integer *maxit,
double x[],
const Integer *ldx,
Integer *iter,
Integer *feval,
Double *nrmgrd,
Integer *ifail,
const Charlen length_opt
)We begin again by loading the FFI namespace and defining our arguments as vectors. Note that the char argument opt is also defined as a vector with one element. The associated string length argument length_opt must be defined as an atom, and not a vector of length one, since it must be passed by value to the routine.
/ Load FFI namespace
\l ffi.q
/ Parameters
g:16#2.0 -1.0 0.0 0.0 -1.0 2.0 -1.0 0.0
0.0 -1.0 2.0 -1.0 0.0 0.0 -1.0 2.0f
ldg:1#4j
n:1#4j
opt:1#"B"
alpha:1#0.02f
w:4#100.0 20.0 20.0 20.0f
errtol:1#0.0f
maxits:1#0j
maxit:1#0j
x:16#0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0f
ldx:1#4j
iter:1#0j
feval:1#0j
nrmgrd:1#0.0f
ifail:1#0j
length_opt:1jTo call the NAG routine using pure q, we again invoke the cf function, passing the desired function symbol name and its return type as arguments, followed by the argument list for the NAG routine.
/ Call NAG routine g02ab
.ffi.cf[(" ";`libnagc_nag.so`g02abf_)]
(g;ldg;n;opt;alpha;w;errtol;maxits;maxit;x;
ldx;iter;feval;nrmgrd;ifail;length_opt)Example Three: Quadratic Programming Optimization
With our final example, we demonstrate how to use an interior point method (IPM) optimization solver to approximate a solution to a quadratic programming (QP) problem of the form
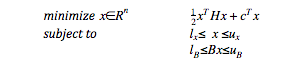
where n is the number of decision variables, m is the number of linear constraints, H is a symmetric n-by-n matrix, x,c,lx and ux are n-dimensional vectors, lB and uB are m-dimensional vectors, and B is an m-by-n matrix.
When invoking NAG Library routine e04st through the alternative C interface, the user is required to supply six callback routines: objfun, objgrd, confun, congrd, hess, and mon. If the user wishes to not explicitly define any, or all, of these callbacks (as we do for this example), the user must instead supply the corresponding ‘dummy’ routine (included with the NAG Library) as the argument for each omitted callback.
Note that using the e04st solver in the manner described above will restrict its applicability to linear and quadratic objective functions and will not allow for nonlinear constraints.
Additionally, we will need to call six additional NAG ‘helper’ routines so that we may initialize the problem handle, add the objective function and constraints to the problem, display the properties of the problem handle, and delete the problem handle by releasing the memory associated with it.
To set up our optimization problem, our first step is to initialize an empty problem handle with a call to NAG Library routine e04ra. The alternative C interface signature is below.
void e04raf_ (
void **handle,
const Integer *nvar,
Integer *ifail
)To accommodate the handle argument, we define it as a pointer to an int representing the bitness of the library (e.g. 64-bit int for a 64-bit library). This matching of bitness is necessary to allow for the proper internal memory allocations performed by the NAG Library as we build up our problem handle.
Within our q script, we again begin by loading the FFI namespace, then define our parameters to pass to the e04ra routine.
/ Load FFI namespace
\l ffi.q
/ Parameters
handle:1#0j
n:1#7j
ifail:1#1j
/ Initialize empty problem handle with N variables
.ffi.cf[(" ";`libnagc_nag.so`e04raf_)](handle;n;ifail)The next step is to add the quadratic objective function to the problem handle using NAG Library routine e04rf. The alternative C interface signature and subsequent q code is displayed below.
Alternate C interface signature:
void e04rff_ (
void **handle,
const Integer *nnzc,
const Integer idxc[],
const double c[],
const Integer *nnzh,
const Integer irowh[],
const Integer icolh[],
const double h[],
Integer *ifail
)q code:
/ Number of nonzero elements in the linear term c of objective
function
nnzc:1#7j
/ Definition of sparse structure for the linear term c
idxc:7#1 2 3 4 5 6 7j
c:7#-200.0 -2000.0 -2000.0 -2000.0 -2000.0 400.0 400.0f
/ Number of nonzero elements in the upper triangular quadratic
/ term H
nnzH:1#9j
/ Definition of sparse structure for the quadratic term H
irowH:9#1 2 3 3 4 5 6 6 7j
icolH:9#1 2 3 4 4 5 6 7 7j
H:9#2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0f
/ Add quadratic objective function to problem handle
.ffi.cf[(" ";`libnagc_nag.so`e04rff_)]
(handle;nnzc;idxc;c;nnzH;irowH;icolH;H;ifail)Next, we define simple bounds for the variables and add them to the problem handle using NAG Library routine e04rh.
Alternative C interface signature:
void e04rhf_ (
void **handle,
const Integer *nvar,
const double bl[],
const double bu[],
Integer *ifail
)q code:
/ Define the lower and upper bounds for variables
l_x:7#0.0 0.0 400.0 100.0 0.0 0.0 0.0f
u_x:7#200.0 2500.0 800.0 700.0 1500.0 1.0e25 1.0e25f
/ Add simple bounds to problem handle
.ffi.cf[(" ";`libnagc_nag.so`e04rhf_)](handle;n;l_x;u_x;ifail)Linear constraints are then added to the problem handle using NAG Library routine e04rj.
Alternative C interface signature:
void e04rjf_ (
void **handle,
const Integer *nclin,
const double bl[],
const double bu[],
const Integer *nnzb,
const Integer irowb[],
const Integer icolb[],
const double b[],
Integer *idlc,
Integer *ifail
)q code:
/ Bounds for linear constraints
m_B:1#7j
l_B:7#-1.0e25 -1.0e25 -1.0e25 -1.0e25 -1.0e25 1500.0 250.0f
u_B:7# 2000.0 60.0 100.0 40.0 30.0 1.0e25 300.0f
/ Sparse structure for linear constraint matrix B
nnzB:1#41j
irowB:41#1 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4
5 5 5 6 6 6 6 6 6 7 7 7 7 7 7 7j
icolB:41#1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 1 2 3 4 5
1 4 5 1 2 3 4 5 6 1 2 3 4 5 6 7j
B:41#1.00 1.00 1.00 1.00 1.00 1.00 1.00
0.15 0.04 0.02 0.04 0.02 0.01 0.03
0.03 0.05 0.08 0.02 0.06 0.01
0.02 0.04 0.01 0.02 0.02
0.02 0.03 0.01
0.70 0.75 0.80 0.75 0.80 0.97
0.02 0.06 0.08 0.12 0.02 0.01 0.97f
/ Additional parameter for e04rjf
idlc:1#0j
/ Add linear constraints to problem handle
.ffi.cf[(" ";`libnagc_nag.so`e04rjf_)]
(handle;m_B;l_B;u_B;nnzB;irowB;icolB;B;idlc;ifail)To verify that our problem handle has been defined correctly, we can display its contents using NAG Library routine e04ry.
Alternative C interface signature:
void e04ryf_ (
void **handle,
const Integer *nout,
const char *cmdstr,
Integer *ifail,
const Charlen length_cmdstr
)q code:
/ Parameters
nout:1#6j
str:"overview; simple bounds; objective; linear constraints bounds;
linear constraints detailed; options"
len_str:99j
/ Display contents of problem handle
.ffi.cf[(" ";`libnagc_nag.so`e04ryf_)]
(handle;nout;str;ifail;len_str)Our next step is to invoke the e04st solver. As mentioned previously, the alternative C interface for NAG routine e04st requires six callback routines, which can be seen below.
void e04stf_ (
void **handle,
void (NAG_CALL *objfun)(const Integer *nvar, const double x[],
double *fx, Integer *inform, Integer iuser[],
double ruser[], void **cpuser
),
void (NAG_CALL *objgrd)(const Integer *nvar, const double x[],
const Integer *nnzfd, double fdx[],
Integer *inform, Integer iuser[], double ruser[],
void **cpuser
),
void (NAG_CALL *confun)(const Integer *nvar, const double x[],
const Integer *ncnln, double gx[],Integer *inform,
Integer iuser[], double ruser[], void **cpuser
),
void (NAG_CALL *congrd)(const Integer *nvar, const double x[],
const Integer *nnzgd, double gdx[],Integer *inform,
Integer iuser[], double ruser[], void **cpuser
),
void (NAG_CALL *hess)(const Integer *nvar, const double x[],
const Integer *ncnln, const Integer *idf,
const double *sigma, const double lambda[],
const Integer *nnzh, double hx[], Integer *inform,
Integer iuser[], double ruser[], void **cpuser
),
void (NAG_CALL *mon)(const Integer *nvar, const double x[],
const Integer *nnzu, const double u[], Integer *inform,
const double rinfo[], const double stats[],
Integer iuser[], double ruser[], void **cpuser
),
const Integer *nvar,
double x[],
const Integer *nnzu,
double u[],
double rinfo[],
double stats[],
Integer iuser[],
double ruser[],
void **cpuser,
Integer *ifail
)To pass the ‘dummy’ routines to the e04st solver using FFI, each callback argument should be specified as a mixed list with the form (func;arg_types;return_types), where func is the symbol name of the function, arg_types is a char array containing the argument types of the function, and return_type is a char matching the return type of the function (” “; for a C void function). The symbol name for each ‘dummy’ routine includes the name of the shared object in which they are located.
/ Initial starting point
x:7#0.0f
/ Additional parameters for IPM solver
n_u:1#0j
u:1#0j
rinfo:32#0.0f / vector of length 32
stats:32#0.0f / vector of length 32
iuser:1#0j
ruser:1#0j
cpuser:1#0j / same type as 'handle'
/ Invoke NAG Interior Point Method solver
.ffi.cf[(" ";`libnagc_nag.so`e04stf_)]
(handle;
(`libnag_nag.so`e04stv_; 1#"iffiifi"; " "); / OBJFUN
(`libnag_nag.so`e04stw_; 1#"ififiifi"; " "); / OBJGRD
(`libnag_nag.so`e04stx_; 1#"ififiifi"; " "); / CONFUN
(`libnag_nag.so`e04sty_; 1#"ififiifi"; " "); / CONGRD
(`libnag_nag.so`e04stz_; 1#"ifiiffifiifi"; " "); / HESS
(`libnag_nag.so`e04stu_; 1#"ifififfifi"; " "); / MON
n;x;n_u;u;rinfo;stats;iuser;ruser;cpuser;ifail
)Finally, we need to destroy the problem handle and deallocate all memory stored within it using NAG Library routine e04rz.
Alternative C interface signature:
void e04rzf_ (
void **handle,
Integer *ifail
)q code:
/ Destroy problem handle and deallocate memory
.ffi.cf[(" ";`libnagc_nag.so`e04rzf_)](handle;ifail)Conclusion
The new Foreign Function Interface (FFI) extension to the q programming language enables kdb+ users to easily integrate the functionality of the NAG Library with kdb+. Software developers can now experience shorter development times, writing less code and employing fewer development tools by following the procedure described in this report.
To obtain the example scripts for the enclosed example programs, please visit the NAG GitHub webpage, or contact NAG Support at support@nag.com.












